因为力扣没有剑指了,所以只能去牛客刷了,我草
PS:有的和力扣烧鸡100重复了,跳过
链表部分
从尾到头打印链表
public class Solution {
ArrayList<Integer> list=new ArrayList<Integer>();
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ListNode p=listNode;
if(p!=null)
{
printListFromTailToHead(p.next);
list.add(p.val);
}
return list;
}
}一开始把list写函数里面了,大错特错
反转链表
public ListNode ReverseList (ListNode head) {
// write code here
ListNode l=null;
ListNode m=head;
while(m!=null)
{
ListNode r=m.next;
m.next=l;
l=m;
m=r;
}
return l;
}一开始return的m,后来发现m都null了,return锤子
合并两个排序的链表
这题比较简单,弱智思路一个一个比就行了,然后最后把剩下的全加上去
public ListNode Merge (ListNode pHead1, ListNode pHead2) {
// write code here
ListNode dummy=new ListNode(0);
ListNode p=dummy;
while(pHead1!=null&&pHead2!=null)
{
if(pHead1.val<=pHead2.val)
{
p.next=pHead1;
pHead1=pHead1.next;
}else
{
p.next=pHead2;
pHead2=pHead2.next;
}
p=p.next;
}
while(pHead1!=null)
{
p.next=pHead1;
p=p.next;
pHead1=pHead1.next;
}
while(pHead2!=null)
{
p.next=pHead2;
p=p.next;
pHead2=pHead2.next;
}
return dummy.next;
}两个链表的第一个公共结点
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
ListNode p1=pHead1;ListNode p2=pHead2;
int lenp1=0;
while(p1!=null)
{
p1=p1.next;
lenp1++;
}
int lenp2=0;
while(p2!=null)
{
p2=p2.next;
lenp2++;
}
p1=pHead1;p2=pHead2;
if(lenp1>lenp2)
{
int k=lenp1-lenp2;
while(k>0)
{
p1=p1.next;
k--;
}
}else
{
int k=lenp2-lenp1;
while(k>0)
{
p2=p2.next;
k--;
}
}
while(p1!=p2)
{
p1=p1.next;
p2=p2.next;
}
return p1;
}长的先走
链表中倒数最后k个结点
public ListNode FindKthToTail (ListNode pHead, int k) {
// write code here
if(pHead==null)return null;
ListNode p=pHead;
ListNode q=pHead;
int len=0;
ListNode m=pHead;
while(m!=null)
{
len++;
m=m.next;
}
if(len<k)return null;
while(k>0)
{
q=q.next;
k--;
}
while(q!=null)
{
q=q.next;
p=p.next;
}
return p;
}老生常谈的题目了,注意pHead为空的情况
链表中环的入口结点
反正有个公式,背吧懒得推导
总的来说就是
1.先判断与有无环,套路
2.把fast放到head结点,和slow一起一个一个走,相遇为入口节点
为什么呢,不知道
public ListNode EntryNodeOfLoop(ListNode pHead) {
if(pHead==null)
return null;
ListNode slow=pHead;
ListNode fast=pHead;
while(fast!=null&&fast.next!=null)
{
fast=fast.next.next;
slow=slow.next;
if(slow==fast)
break;
}
if(fast==null||fast.next==null)return null;
fast=pHead;
// 与第一次相遇的结点相同速度出发,相遇结点为入口结点
while(fast!=slow)
{
fast=fast.next;
slow=slow.next;
}
return fast;
}删除链表的节点
public ListNode deleteNode (ListNode head, int val) {
// write code here
if(head==null)return null;
ListNode p=head;
if(p.val==val)
{
return head.next;
}
while(p.next!=null)
{
if(p.next.val==val)//注意,这里直接把p当pre用就行了,也就是说判断P.next是不是val即可
{
ListNode q=p.next;
p.next=q.next;
q.next=null;
return head;
}
p=p.next;
}
return null;
}注意第一个节点
删除链表中重复的结点
public ListNode deleteDuplication(ListNode head) {
ListNode dummy=new ListNode(-1);
ListNode tail=dummy;
while(head!=null)
{
if(head.next==null||head.next.val!=head.val)
{
tail.next=head;
tail=head;
}
while(head.next!=null&&head.next.val==head.val)head=head.next;
head=head.next;
}
tail.next=null; //这一步至关重要,比如12233455,如果最后不断掉,那么会返回1455
return dummy.next;
}我一开始的傻逼想法:用set,false了就删掉,后来发现这样能保留第一个重复的节点,我是傻逼
树
二叉树的深度
经典递归,反正等于子树高度加一
public int TreeDepth(TreeNode root) {
if(root==null)return 0;//这一句一写还用考虑left,right=null吗?
else
return Math.max(TreeDepth(root.left),TreeDepth(root.right))+1;
}按之字形顺序打印二叉树
注意点:
1.如何判断一层:队列size
2.如何实现”之“,直接用Collections.reverse(),就不用麻烦的后端插入Arraylist和前端插入Arraylist了
public ArrayList<ArrayList<Integer>> Print (TreeNode pRoot) {
// 思路:双端队列,奇数层翻转(从0开始),偶数层不翻转
ArrayList<ArrayList<Integer>> res=new ArrayList<>();
if(pRoot==null)return res;
Deque <TreeNode>dq=new LinkedList<TreeNode>();
boolean flag=true;
dq.offer(pRoot);
while(!dq.isEmpty())
{
ArrayList<Integer> aa=new ArrayList<>();
int n=dq.size();//这一层有多少node
flag=!flag;
for(int i=0;i<n;i++)
{
TreeNode p=dq.pollFirst();
aa.add(p.val);
if(p.left!=null)
dq.offer(p.left);
if(p.right!=null)
dq.offer(p.right);
}
if(flag)
{
Collections.reverse(aa);
}
res.add(aa);
}
return res;
}二叉搜索树的第k个节点
ArrayList<Integer>res=new ArrayList<>();
public int KthNode (TreeNode proot, int k) {
if(proot==null||k==0)return -1;//空,或者没k
mid(proot);//中序遍历获得升序数组
if(k>res.size())return -1;//没这么多node
return res.get(k-1);
}
public void mid(TreeNode root)
{
if(root==null)return;
mid(root.left);
res.add(root.val);
mid(root.right);
}知识点:二叉搜索树中序遍历为升序序列
重建二叉树
这题力扣烧鸡100也有,之前就稀里糊涂过去了
额其实842期末也有,但当时也是稀里糊涂过去了
注意点放注释里了
这个是力扣是上我写的,傻逼牛客有问题,算了
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeHelper(preorder,0,preorder.length,inorder,0,inorder.length);
}
public TreeNode buildTreeHelper(int[]preorder,int pstart,int pend,int []inorder,int istart,int iend)
{
//pstart:前序数组中左子树的开头,pend:前序数组中左子树的结束,左闭右开
//istart:终须数组中左子树的开头,iend:终须数组中左子树的结束,左闭右开
if(pstart==pend)
return null;
int root_val=preorder[pstart];//前序数组第一个为更节点
TreeNode root=new TreeNode(root_val);
int iroot_index=0;//中序遍历中根节点的位置
for(int i=istart;i<iend;i++)
{
if(root_val==inorder[i])
{
iroot_index=i;
break;
}
}
int lefnum=iroot_index-istart;//左子树的长度,等于中序遍历中,根节点的位置减去开头
root.left=buildTreeHelper(preorder,pstart+1,pstart+lefnum+1,inorder,istart,iroot_index);
root.right=buildTreeHelper(preorder,pstart+lefnum+1,pend,inorder,iroot_index+1,iend);
return root;
}树的子结构
这题目很好,思路是什么
1.b是子结构,那么b的左右子树也就是a的左右子树的子结构
2.所以怎么办,递归的从a中寻找b的根节点看能不能找到,能找到那么则比较其左右子树是不是子结构即可
public class Solution {
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
//思路:递归,root2是子哦结构,那么root2的左右子树也都是子结构
//所以我们先找roo1和root2相等的,然后找root1的左右子树有没有
//返回条件是什么?有空
return (root1!=null&&root2!=null)&&(recur(root1,root2)||HasSubtree(root1.left,root2)||HasSubtree(root1.right,root2));
}
//详解:因为要判断b是不是a的,所以b肯定比a小
//所以这里比较子结构,其实就是一个一个去比较值等不等,等的话就再去递归判断他的左右子树上节点等不等
//这里是比较两个部分是不是对应的子结构
public boolean recur(TreeNode a,TreeNode b)
{
if(b==null)return true;//说明b已经比较完了,下面没了,那么说明是真
if(a==null||a.val!=b.val)return false;//如果a为空,也就是说a不够长了,或者值不相等,那么肯定不是
return recur(a.left,b.left)&&recur(a.right,b.right);
}
}二叉树的镜像
这题就是普通递归交换左右子树,但是牛客这个有点傻逼,非要我return一个什么东西
我return牛魔
public TreeNode Mirror (TreeNode root) {
TreeNode p=root;
if(root == null) {
return null;
}
if(root.left == null && root.right == null) {
return root;
}
TreeNode temp = root.left;
root.left = root.right;//这样把整个子树也都交换过去了
root.right = temp;
Mirror(root.left);
Mirror(root.right);
return p;
}从上往下打印二叉树
byd这牛客给这个例子我都没看明白
这不就是层序遍历么?
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer>res=new ArrayList<>();
if(root==null)
return res;
Queue<TreeNode>q=new ArrayDeque<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode cur=q.poll();
res.add(cur.val);
if(cur.left!=null)
q.offer(cur.left);
if(cur.right!=null)
q.offer(cur.right);
}
return res;
}二叉搜索树的后序遍历序列
这题很容易想到分治法,但我还是不熟悉用helper
and终止条件没把握,我是傻逼
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence.length==0)return false;
return recur(sequence,0,sequence.length-1);
}
public boolean recur(int []sequence,int i,int j)
{
if(i>=j)return true;//i>=j说明此子树结点数<=1,不用判断了
int p=i;
while(sequence[p]<sequence[j])p++;//sequence[len-1]为root
int m=p;//m为第一个大于root值的位置,讲sequece分割为左右子树了[i,m-1]
while(sequence[p]>sequence[j])p++;
//此时p为第一个小于root值的位置,分割为[m,p]
//按理来说,p应该等于j,因为小于sequence[j]的都应该在左子树当中
//如果不等于,说明错了
return (p==j)&&recur(sequence,i,m-1)&&recur(sequence,m,j-1);
}
}二叉树中和为某一值的路径(一)
我卡在哪里了:在想如果超过了怎么把前面的吐出来
解决办法:不用吐出来,没遍历到一个,tmpsum加p.val,然后比较即可
wait,此题定义路径为根节点到叶子结点,那么更不不需要讨论吐出来。。。我是傻逼
用加的,不用减的,超过了和没超过一样的,反正都是不等于
public class Solution {
private static int sumVal=-1;
private boolean flag=false;
public boolean hasPathSum (TreeNode root, int sum) {
sumVal=sum;
// write code here
dfs(root,0);
return flag;
}
public void dfs(TreeNode p, int tmpsum)
{
if(p==null)return;
if(p.left!=null)
{
dfs(p.left,tmpsum+p.val);
}
if(p.left==null&&p.right==null)
{
boolean tmpflag=tmpsum+p.val==sumVal;
flag=flag||tmpflag;//防止别的路径已经找到了,但是被新的false覆盖
}
if(p.right!=null)
{
dfs(p.right,tmpsum+p.val);
}
}
}二叉树中和为某一值的路径(二)
这题又让我练了一下回溯法
import java.util.*;
public class Solution {
//回溯法+二叉树题目
//回溯法不知道几部了,反正就是定义回溯函数,然侯加入,然后回调
public ArrayList<ArrayList<Integer>> FindPath (TreeNode root, int target) {
ArrayList<ArrayList<Integer>> res=new ArrayList<>();
ArrayList<Integer> path=new ArrayList<>();
if(root==null)return res;
preorderdfs(root,target,res,path);//定义函数
return res;
}
public void preorderdfs(TreeNode root,int targetsum,ArrayList<ArrayList<Integer>> res,ArrayList<Integer> path)
{
path.add(root.val);//加入
if(root.left==null&&root.right==null)
{
if(targetsum-root.val==0)
{
res.add(new ArrayList<>(path));//这里一定要这么写,为什么我不知道
}
return;/*
为什么这里不remove呢,因为我们remove的操作实在回溯了之后的那个语句做的,发现没有
终止条件:找到叶子结点了,但是和不是target,终止
*/
}
if(root.left!=null)
{
preorderdfs(root.left,targetsum-root.val,res,path);
path.remove(path.size()-1);//回溯
}
if(root.right!=null)
{
preorderdfs(root.right,targetsum-root.val,res,path);
path.remove(path.size()-1);//回溯
}
}
}二叉搜索树与双向链表
我妄想用一个指正解决问题,那不可能
public TreeNode head = null;
//中序遍历当前值的上一位,初值为最小值,先定为null
public TreeNode pre = null;
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree == null)
//中序递归,叶子为空则返回
return null;
//首先递归到最左最小值
Convert(pRootOfTree.left);
//找到最小值,初始化head与pre
if(pre == null){
head = pRootOfTree;
pre = pRootOfTree;
}
//当前节点与上一节点建立连接,将pre设置为当前值
else{
pre.right = pRootOfTree;
pRootOfTree.left = pre;
pre = pRootOfTree;
}
Convert(pRootOfTree.right);
return head;
}判断是不是平衡二叉树_
此题很简单吗,先递归求高度,然后递归求是不是平衡
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return bool布尔型
*/
public boolean IsBalanced_Solution (TreeNode pRoot) {
// write code here
if(pRoot==null)
return true;
int leftdeep=deep(pRoot.left);
int rightdeep=deep(pRoot.right);
if(leftdeep-rightdeep>1||leftdeep-rightdeep<-1)
return false;
return IsBalanced_Solution(pRoot.left)&&IsBalanced_Solution(pRoot.right);
}
public int deep(TreeNode root)
{
if(root==null)
return 0;
return Math.max(deep(root.left),deep(root.right))+1;
}
}二叉树的下一个结点
分情况讨论:
- 如果给出的结点有右子节点,则最终要返回的下一个结点即右子树的最左下的结点
- 如果给出的结点无右子节点,且当前结点是其父节点的左子节点,则返回其父节点
- 如果给出的结点无右子节点,且当前结点是其父节点的右子节点,则先要沿着左上方父节点爬树,一直爬到当前结点是其父节点的左子节点为止,返回的就是这个父节点;或者没有满足上述情况的则返回为NULL
public TreeLinkNode GetNext(TreeLinkNode node) {
if(node.right!=null)
{
TreeLinkNode p=node.right;
while(p.left!=null)
{
p=p.left;
}
return p;
}
if(node.next!=null&&node.next.left==node)
{
return node.next;
}
if(node.next!=null)
{
TreeLinkNode p=node.next;
while(p.next!=null&&p.next.right==p)p=p.next;
return p.next;
}
return null;
}对称的二叉树
我的一个误区:最小元比较时还在判断left和right,然而只要比较值是不是相等就行了
public class Solution {
public boolean isSymmetrical (TreeNode pRoot) {
if(pRoot==null)return true;
// write code here
return Helper(pRoot.left,pRoot.right);
}
public boolean Helper(TreeNode r1,TreeNode r2)
{
if(r1==null&&r2==null)return true;
if(r1==null||r2==null||r1.val!=r2.val)//就是这里,直接比较值就行了,不要比较left.val什么的
{
return false;
}
return Helper(r1.left,r2.right)&&Helper(r1.right,r2.left);
}
}把二叉树打印成多行
和“之字型打印“是一个道理
只要记住:判断是否已经一行,int n=dq.size()即可
public ArrayList<ArrayList<Integer>> Print (TreeNode pRoot) {
// write code here
Deque<TreeNode> dq=new LinkedList<TreeNode>();
ArrayList<ArrayList<Integer>>res=new ArrayList<>();
if(pRoot==null)return res;
dq.offer(pRoot);
while(!dq.isEmpty())
{
ArrayList<Integer>ans=new ArrayList<>();
int n=dq.size();
for(int i=0;i<n;i++)
{
TreeNode p=dq.pollFirst();
ans.add(p.val);
if(p.left!=null)
dq.offer(p.left);
if(p.right!=null)
dq.offer(p.right);
}
res.add(new ArrayList<>(ans));
}
return res;
}在二叉树中找到两个节点的最近公共祖先
此题很重要,建议每次做都看一下力扣的解答
栈
用两个栈实现队列
没什么高级的,就是pop时把一个栈全pop到另一个栈里,在pop。。。
public:
void push(int node) {
stack1.push(node);
}
int pop() {
while(!stack1.empty())
{
stack2.push(stack1.top());
stack1.pop();
}
int res=stack2.top();
stack2.pop();
while(!stack2.empty())
{
stack1.push(stack2.top());
stack2.pop();
}
return res;
}
private:
stack<int> stack1;
stack<int> stack2;栈的压入、弹出序列
这一题解法的原理是什么?
如果压入和弹出序列是符合的,那么按照这个序列走,一定能走完
所以你只要按照给的顺序走一遍就行了
public boolean IsPopOrder (int[] pushV, int[] popV) {
// write code here
int n=pushV.length;
Stack<Integer>s=new Stack<>();
int j=0;
for(int i=0;i<n;i++)
{
while(j<n&&(s.isEmpty()||s.peek()!=popV[i]))
{
s.push(pushV[j]);
j++;
}
if(s.peek()==popV[i])
{
s.pop();
}else
return false;
}
return true;
}翻转单词序列
熟悉javaapi用的
public String ReverseSentence(String str) {
String []arr=str.split(" ");
Stack<String>stk=new Stack<String>();
for(String s:arr)
{
stk.push(s);
}
StringBuilder res=new StringBuilder();
while(!stk.isEmpty()){
res.append(stk.pop());
res.append(" ");
}
return res.toString().substring(0,res.toString().length()-1);
}滑动窗口的最大值
用优先队列,注意如何创建最大堆
public ArrayList<Integer> maxInWindows (int[] num, int size) {
// write code here
ArrayList<Integer> res=new ArrayList<>();
if(num.length==0||size==0||num.length<size)return res;
PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->o2-o1);
for(int i=0;i<size;i++)pq.add(num[i]);
res.add(pq.peek());
for(int i=1;i+size-1<num.length;i++)
{
pq.remove(num[i-1]);
pq.add(num[i+size-1]);
res.add(pq.peek());
}
return res;
}搜索算法部分
数字在升序数组中出现的次数
private int bisearch(int[] data, double k){
int left = 0;
int right = data.length - 1;
//二分左右界
while(left <= right){
int mid = (left + right) / 2;
if(data[mid] < k)
left = mid + 1;
else if(data[mid] > k)
right = mid - 1;
}
return left;
}
public int GetNumberOfK(int [] array , int k) {
//分别查找k+0.5和k-0.5应该出现的位置,中间的部分就全是k
return bisearch(array, k + 0.5) - bisearch(array, k - 0.5);
}一眼二分,但是我一开始想说递归二分,然后发现只要求左右边界就行了
思路二:直接求左右边界
import java.util.*;
public class Solution {
//思路:二分找左边界,二分找有边界,然后相减即可
public int GetNumberOfK (int[] nums, int k) {
int a=getLeft(nums,k);
int b=getRight(nums,k);
return b-a-1;
}
public int getLeft(int []nums,int k)
{
int l=0,r=nums.length-1;//左臂右臂
while(l<=r)
{
int mid=(l+r)/2;
if(nums[mid]<k)
{
l=mid+1;
}
else
{
r=mid-1;
}
}
return r;
}
public int getRight(int []nums, int k)
{
int l=0,r=nums.length-1;
while(l<=r)
{
int mid=(l+r)/2;
if(nums[mid]>k)
{
r=mid-1;
}else
{
l=mid+1;
}
}
return l;
}
}旋转数组的最小数字
这题和力扣上还不同,这题剑指有相同值,力扣没有
所以这一题,剑指offer的方法更有通用性,掌握这个
public int minNumberInRotateArray (int[] nums) {
//思路:旋转后的数组分为两个部分,也就是两个升序序列
//我们要找的值其实就是第二段升序序列的第一个数
//我们找到mid,然后和nums[j]比较,如果小于他,那么nums[mid]就在第二段序列里
//如果大于他,那么就在第一段序列里,那么更新left
//如果小于他那么就在第二段 序列里面,更新right
int l=0,r=nums.length-1;
while(l<r)//左闭右开
{
int m=(l+r)/2;
if(nums[m]>nums[r])
{
l=m+1;//左边闭区间,所以必须+1
}else if(nums[m]<nums[r])
{
r=m;//右边开区间,所以不用
}else
{
r--;
}
}
return nums[l];
}注意事项在注释里面
二维数组中的查找
public boolean Find (int target, int[][] array) {
// write code here
int i=0,j=array[0].length-1;
while(i<array.length&&j>=0)
{
if(target>array[i][j])
{
i++;
}
else if(target<array[i][j])
{
j--;
}
else
{
return true;
}
}
return false;
}思路啊,三种方法:
- 两层遍历
- 对每个子数组用二分
- 这种方法,鉴定为观察能力极强
字符串的排列_牛客题霸_牛客网 (nowcoder.com)
这个题目要注意的是:字符串里有重复字符,abb’与ab’b,bab’与b’ab,bb’a与b’ba都是重复的,难点在于去除这些重复
由此为了去重,我们可以定义一个规则,即对于相同数,我们人为定序,如上例子中11'2345,我们指定重复数字首次要放入某一个框位时,只能放重复数字的第一个,如这里只能放1,放1'的情况直接过滤,其他框位同理
具体做法:
step 1:先对字符串按照字典序排序,获取第一个排列情况。
step 2:准备一个空串暂存递归过程中组装的排列情况。使用额外的vis数组用于记录哪些位置的字符被加入了。
step 3:每次递归从头遍历字符串,获取字符加入:首先根据vis数组,已经加入的元素不能再次加入了;同时,如果当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用,也不需要将其纳入。
step 4:进入下一层递归前将vis数组当前位置标记为使用过。
step 5:回溯的时候需要修改vis数组当前位置标记,同时去掉刚刚加入字符串的元素,
step 6:临时字符串长度到达原串长度就是一种排列情况。
import java.util.*; public class Solution { public ArrayList<String> Permutation (String str) { // write code here ArrayList<String>res=new ArrayList<>(); char[]charStr=str.toCharArray(); Arrays.sort(charStr); boolean[]visit=new boolean[charStr.length]; StringBuffer temp=new StringBuffer(); back(res,charStr,temp,visit); return res; } public void back(ArrayList<String>res,char[]str,StringBuffer temp,boolean[]visit) { if(temp.length()==str.length) { res.add(new String(temp)); return; } for(int i=0;i<str.length;i++) { if(visit[i]) { continue;//这个元素用过了,跳过 } if(i>0&&str[i-1]==str[i]&&!visit[i-1])//这里表示的是回溯过来的,1 1' 2 3 从1’开始取的情况,这个时候因为回溯了,所以1的visit的false,但是1' 与1会重复,所以不能取 { continue; } visit[i]=true; temp.append(str[i]); back(res,str,temp,visit); visit[i]=false; temp.deleteCharAt(temp.length()-1); } } }
LCR 163. 找到第 k 位数字 - 力扣(LeetCode)
这题有一说一,规律太难找,只能反复刷记住了
public int findKthNumber(int k) {
//k是整个序列中的位置
int digit=1;//位数,一位数二位数这种
long start=1;//每位数的起始数字,就是1,10,100,1000
long count=9;//每种位数的数,各占多少位置,个位数9位,十位数180位
//首先k所在的数字是几位数,一直减掉1、2、3.。。。位数的数量即可
while(k>count)
{
k-=count;
start*=10;
digit+=1;
count=9*start*digit;
}
//减完之后,最后剩下的k其实就是,第k个digit位数(从 0开始)
//然后获得,k所在的是哪一个数字
long num=start+(k-1)/digit;//因为序列从第“0”个数字开始,start是n位数的第一个,也就是10,100,1000.。。然后k-1/digit相当于偏移量
//确定他是哪一位
String s=Long.toString(num);
int res=s.charAt((k-1)%digit)-'0';
return res;
}动态规划
连续子数组的最大和
记住杀卡尔的动态规划五部曲
public int FindGreatestSumOfSubArray (int[] array) {
// write code here
int []dp=new int[array.length];
dp[0]=array[0];
for(int i=1;i<array.length;i++)
{
dp[i]=Math.max(dp[i-1]+array[i],array[i]);
}
int res=Integer.MIN_VALUE;
for(int i=0;i<dp.length;i++)
{
res=Math.max(res,dp[i]);
}
return res;
}连续子数组的最大和(二)
思路其实就是维护left和right,因为要返回最长的,所以还得维护maxleft,maxright
public int[] FindGreatestSumOfSubArray (int[] array) {
// write code here
int len = array.length;
int []dp = new int[len];
ArrayList<Integer>list = new ArrayList<>();
dp[0] = array[0];
int left = 0, right = 0;
int maxleft = 0, maxright = 0;
int maxsum = dp[0];//注意此处初始化
for (int i = 1; i < len; i++) {
right++;
dp[i] = Math.max(dp[i - 1] + array[i], array[i]);
if (dp[i - 1] + array[i] < array[i]) {
left = right; //重置了
}
//遇到新的最大值了
if (dp[i] > maxsum || dp[i] == maxsum &&
(right - left + 1) > (maxright - maxleft + 1)) { //因为要返回最长的
maxsum = dp[i];
maxleft = left;
maxright = right;
}
}
int []res = new int[maxright - maxleft + 1];
for(int i=maxleft,j=0;i<=maxright;i++,j++)
{
res[j]=array[i];
}
return res;
}斐波那契数列
public int Fibonacci (int n) {
// write code here
int []dp=new int [n+1];
dp[1]=1;
dp[2]=1;
for(int i=3;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}礼物的最大价值
比较简单,和机器人走路是一个套路
public int maxValue (int[][] grid) {
// write code here
int m=grid.length;
int n=grid[0].length;
int [][]dp=new int[m][n];
dp[0][0]=grid[0][0];
for(int i=1;i<n;i++)
{
dp[0][i]=dp[0][i-1]+grid[0][i];
}
for(int j=1;j<m;j++)
{
dp[j][0]=dp[j-1][0]+grid[j][0];
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}最长不含重复字符的子字符串
说是动态规划,但我一开始用的暴力
public int lengthOfLongestSubstring (String s) {
// write code here
int left=0,right=1;
if(s.length()==0)return 0;
if(s.length()==1)return 1;
int maxlen=0;
while(right<s.length())
{
if(hassame(s.substring(left,right+1)))
{
left++;
}else
{
maxlen=Math.max(maxlen,right-left+1);
right++;
}
}
return maxlen;
}
public boolean hassame(String s)
{
Set<Character>set=new HashSet<Character>();
for(int i=0;i<s.length();i++)
{
if(!set.add(s.charAt(i)))
{
return true;
}
}
return false;
}后来我自己写的动态规划
public int lengthOfLongestSubstring (String s) {
// write code here
//思路:好像和最大子数组和差不多?
//dp[i]:以i结尾的最长不包含重复字符的子串长度
//dp[i]=dp[i-1]+1,当s.charat(i)不和前面的重复
//否则dp[i]=1
//如何判断充不重复呢
int len=s.length();
int[]dp=new int[len];
dp[0]=1;
int left=0,right=0;
int maxleft=0,maxright=0;
int maxlen=1;
for(int i=1;i<len;i++)
{
right++;
char c=s.charAt(i);
if(s.substring(left,right).indexOf(c)>=0)
{
dp[i]=1;
left=right;
}else
{
dp[i]=dp[i-1]+1;
if(right-left+1>maxlen)
{
maxlen=right-left+1;
maxleft=left;
maxright=right;
}
}
}
return maxlen;
}又错了,发现错哪了吗
更新left的时候,我们应该更新到重复元素的第一个个左边,而不是直接更新到right
修改:
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @return int整型
*/
public int lengthOfLongestSubstring (String s) {
// write code here
//思路:好像和最大子数组和差不多?
//dp[i]:以i结尾的最长不包含重复字符的子串长度
//dp[i]=dp[i-1]+1,当s.charat(i)不和前面的重复
//否则dp[i]=1
//如何判断充不重复呢
int len=s.length();
int[]dp=new int[len];
dp[0]=1;
int left=0,right=0;
int maxleft=0,maxright=0;
int maxlen=1;
for(int i=1;i<len;i++)
{
right++;
char c=s.charAt(i);
int index=s.indexOf(c,left);
if(index>=left&&index<right)//修改部分
{
dp[i]=1;
left=index+1;
}else
{
dp[i]=dp[i-1]+1;
if(right-left+1>maxlen)
{
maxlen=right-left+1;
maxleft=left;
maxright=right;
}
}
}
return maxlen;
}
}力扣上给了我们滑动窗口的方法
public int lengthOfLongestSubstring(String s) {
HashMap<Character, Integer> map = new HashMap<>();
int maxLen = 0;//用于记录最大不重复子串的长度
int left = 0;//滑动窗口左指针
for (int i = 0; i < s.length() ; i++)
{
/**
1、首先,判断当前字符是否包含在map中,如果不包含,将该字符添加到map(字符,字符在数组下标),
此时没有出现重复的字符,左指针不需要变化。此时不重复子串的长度为:i-left+1,与原来的maxLen比较,取最大值;
2、如果当前字符 ch 包含在 map中,此时有2类情况:
1)当前字符包含在当前有效的子段中,如:abca,当我们遍历到第二个a,当前有效最长子段是 abc,我们又遍历到a,
那么此时更新 left 为 map.get(a)+1=1,当前有效子段更新为 bca;
2)当前字符不包含在当前最长有效子段中,如:abba,我们先添加a,b进map,此时left=0,我们再添加b,发现map中包含b,
而且b包含在最长有效子段中,就是1)的情况,我们更新 left=map.get(b)+1=2,此时子段更新为 b,而且map中仍然包含a,map.get(a)=0;
随后,我们遍历到a,发现a包含在map中,且map.get(a)=0,如果我们像1)一样处理,就会发现 left=map.get(a)+1=1,实际上,left此时
应该不变,left始终为2,子段变成 ba才对。
为了处理以上2类情况,我们每次更新left,left=Math.max(left , map.get(ch)+1).
另外,更新left后,不管原来的 s.charAt(i) 是否在最长子段中,我们都要将 s.charAt(i) 的位置更新为当前的i,
因此此时新的 s.charAt(i) 已经进入到 当前最长的子段中!
*/
if(map.containsKey(s.charAt(i)))
{
left = Math.max(left , map.get(s.charAt(i))+1);
}
//不管是否更新left,都要更新 s.charAt(i) 的位置!
map.put(s.charAt(i) , i);
maxLen = Math.max(maxLen , i-left+1);
}
return maxLen;
}其实这个方法就是用i,代替了right
把数字翻译成字符串
public int solve (String nums) {
if(nums.length()==0||nums.charAt(0)=='0')
return 0;
int []dp=new int[nums.length()];
dp[0]=1;
for(int i=1;i<dp.length;i++)
{
if(nums.charAt(i)!='0')
{
dp[i]=dp[i-1];//先默认都一样
}
int num=(nums.charAt(i-1)-'0')*10+(nums.charAt(i)-'0');//计算自己和前一个平起来的两位数
if(num>=10&&num<=26)
{
//如果在范围内可以表示
if(i==1)
dp[i]+=1;
else
dp[i]+=dp[i-2];
}
}
return dp[nums.length()-1];
}有条件的青蛙跳台阶问题,需要判断i-1和i组成的二位数是否可以表示,这里的关键在于如何处理“0
10. 正则表达式匹配 - 力扣(LeetCode)
这题目太他妈难了,面试之前突击一下吧
public boolean isMatch(String s, String p) {
//dp[i][j],s0 i-1,是否匹配p 0 ,j-1这样方便初始化
//这题也太他妈难了
if(s==null||p==null)return false;
int slen=s.length(),plen=p.length();
boolean[][]dp=new boolean[slen+1][plen+1];
dp[0][0]=true;
for(int j=1;j<plen+1;j++)
{
if(p.charAt(j-1)=='*')dp[0][j]=dp[0][j-2];//s是空串,如果j-1的位置是*,那么就把j-2删掉,再比较前面的
}
for(int i=1;i<slen+1;i++)
{
for(int j=1;j<plen+1;j++)
{
if(s.charAt(i-1)==p.charAt(j-1)||p.charAt(j-1)=='.')//如果相等或者j是点,因为点可以任意匹配,
{
dp[i][j]=dp[i-1][j-1];
}else if(p.charAt(j-1)=='*')//如果是*,那么得看i-1和j-2匹不匹配
{
if(s.charAt(i-1)==p.charAt(j-2)||p.charAt(j-2)=='.')
{
dp[i][j]=dp[i][j-2]||dp[i-1][j-2]||dp[i-1][j];
}else{
dp[i][j]=dp[i][j-2];
}
}
}
}
return dp[slen][plen];
}排序算法
数组中重复的数字
public int duplicate (int[] numbers) {
// write code here
HashSet<Integer>set=new HashSet<Integer>();
for(int i=0;i<numbers.length;i++)
{
if(!set.add(numbers[i]))
{
return numbers[i];
}
}
return -1;
}用set,鉴定为易
最小的K个数
public ArrayList<Integer> GetLeastNumbers_Solution (int[] input, int k) {
// write code here
ArrayList<Integer>list=new ArrayList<Integer>();
Arrays.sort(input);
for(int i=0;i<k;i++)
{
list.add(input[i]);
}
return list;
}· 以上 为弱智解法
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param input int整型一维数组
* @param k int整型
* @return int整型ArrayList
*/
public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
ArrayList<Integer> res = new ArrayList<>(k);
//根据题意要求,如果K>数组的长度,返回一个空的数组
if (k > input.length || k == 0)
return res;
quickSort(input, res, k, 0, input.length - 1);
return res;
}
private void quickSort(int[] input, ArrayList<Integer> res, int k, int left, int right) {
//快排的实现方式有多种,我们选择了其中的一种
int start = left;
int end = right;
while (left < right) {
while (left < right && input[right] >= input[start]) {
right--;
}
while (left < right && input[left] <= input[start]) {
left++;
}
swap(input, left, right);
}
swap(input, left, start);
//注意这里,start是数组中元素的下标。在start之前的元素都是比start指向的元素小,
//后面的都是比他大。如果k==start,正好start之前的k个元素是我们要找的,也就是
//数组中最小的k个,如果k>start,说明前k个元素不够,我们还要往后再找找。如果
//k<start,说明前k个足够了,我们只需要在start之前找k个即可。
if (left > k) {
quickSort(input, res, k, start, left - 1);
} else if (left < k) {
quickSort(input, res, k, left + 1, end);
} else {
//取前面的k个即可
for (int m = 0; m < k; ++m) {
res.add(input[m]);
}
}
}
private void swap(int[] arr, int i, int j) {
if (i == j)
return;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}· 快排,一次排序可以确认pivot在排序后的数组里的位置,只要比较这个位置和k即可
然而还有更好的方法,那就是堆排序
public ArrayList<Integer> GetLeastNumbers_Solution (int[] input, int k) {
// write code here
PriorityQueue<Integer>pq=new PriorityQueue<>();//默认创建是小顶堆
for(int i=0;i<input.length;i++)
{
pq.add(input[i]);
}
ArrayList<Integer>res=new ArrayList<>();
while(k>0)
{
res.add(pq.peek());
pq.poll();
k--;
}
return res;
}数组中的逆序对
弱智方法一:
冒泡排序,记录总共交换了多少次
经典最后一个用例超时
public int InversePairs (int[] nums) {
// write code here
int res=0;
for(int i=0;i<nums.length-1;i++)
{
for(int j=0;j<nums.length-i-1;j++)
{
if(nums[j]>nums[j+1])
{
swap(nums,j,j+1);
res++;
}
}
}
return res;
}
public void swap(int nums[],int i,int j)
{
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}归并排序法:归并排序爷还不熟,后面继续熟悉
class Solution {
int count=0;
public int reversePairs(int[] nums) {
this.count=0;
mergeSort(nums,0,nums.length-1);
return count;
}
public void mergeSort(int []nums,int left,int right)
{
if(left>=right)return ;
int mid=(left+right)/2;
mergeSort(nums,left,mid);
mergeSort(nums,mid+1,right);
merge(nums,left,mid,right);
}
public void merge(int []nums,int left,int mid,int right)
{
int []tmp=new int[right-left+1];
int i=left;
int j=mid+1;
int t=0;
while(i<=mid&&j<=right)
{
if(nums[i]<=nums[j])
{
tmp[t++]=nums[i++];
}else
{
count+=mid-i+1;
tmp[t++]=nums[j++];
}
}
while(i<=mid)
tmp[t++]=nums[i++];
while(j<=right)
tmp[t++]=nums[j++];
for(int k=0;k<tmp.length;k++)
nums[left+k]=tmp[k];
}
}数据流中的中位数_牛客题霸_牛客网 (nowcoder.com)
这个思路很无敌,一个最小堆一个最大堆,那么两个的头就是中间的元素
public class Solution {
PriorityQueue<Integer> max=new PriorityQueue<>();//保存较大的一般
PriorityQueue<Integer> min=new PriorityQueue<>((o1,o2)->o2.compareTo(o1));
//保存较小的一半
public void Insert(Integer num) {
min.offer(num);//先进较小的一半
max.offer(min.poll());//然后把较小的里面最大的弄到较大的一半里面
//因为java里/2是四舍五入的,所以要保证较小的一半比较大的一半不少
if(min.size()<max.size())
min.offer(max.poll());
}
public Double GetMedian() {
if(min.size()>max.size())//大,说明是奇数个
{
return(double) min.peek();
}
else//相等,说明是偶数个
{
return (double)(min.peek()+max.peek())/2;
}
}位运算部分
傻逼位运算是最恶心的题目,我操你妈
数值的整数次方
思路:快速幂方法
计算x64,可以直接,x,x2,x4,x8….
计算x77,可以直接x,x2,x4…..x76,最后再乘x得到x77
但是你从左往右你怎么知道要不要乘x呢
所以我们倒过来求,对于x(a),我们求x(a/2) =yjava中是向下取整
要是a为偶数,xa=y2,要是是奇数,xa=y2*x
即可
//为了防止坑爹用力,把n变成long
public class Solution {
public double Power(double x, int n) {
long N =n;
return N>=0?quick(x,N):1.0/quick(x,-N);
}
public double quick(double x, long n)
{
if(n==0)return 1.0;
double y=quick(x,n/2);
return n%2==0?y*y:y*y*x;
}
}求1+2+3+…+n
方法一:没说不能用递归啊,那我们可以直接递归
public int Sum_Solution(int n) {
return n==0?0:Sum_Solution(n-1)+n;
}二进制中1的个数
记住:有一个性质:n&(n-1)可以消除二进制表示的n中最后的一个1,反正你记住就行了
public int NumberOf1 (int n) {
// write code here
int res=0;
while(n!=0)
{
res+=1;
n=n&(n-1);//不断这样,直到n里1全没了,那就是n变成0了
}
return res;
}数组中只出现一次的两个数字
首先题目对空间复杂度有要求,所以不能用哈希表
我们知道,数组中只出现一次的一个数字,可以直接将数组里所有的数异或(^) 利用异或同0异1的性质求出来
但是此处是两个数字,怎么办呢
知识点:x&-x可以取出二进制x中最低位的那个1
那么我们要把数字分为两类
如果我们任然将所有的数字都异或,得到一个x,那么他就是只出现一次的两个数字x1与x2的异或
然后我们将x&-x,得到它最低位的那个1,我们假设这一位是k位
因为是二进制,所以所有数的k位只有两种可能,1或者0
这样把所有的数分成了两类,一类是k位是0,一类是k位是1
因为除了x1,x2 其他都出现了两次
所以出现了两次的数,会被分在同一类中,而因为x1异或x2,也就是x第k位是1,所以x1和X2的第k位必然不同
所以x1与x2会被分为不同的类当中
public int[] FindNumsAppearOnce (int[] nums) {
// write code here
int xorsum=0;
for(int num:nums)
{
xorsum^=num;
}
int lsb=(xorsum==Integer.MIN_VALUE?xorsum:xorsum&(-xorsum));//xorsum是-2147483648的时候变为正数会溢出,因为32位的int正数范围是0~2147483647,而为什么是min.value时,直接返回xorsum呢,因为-2147483638二进制是1000000000,最低位的1其实就是她自己
int t1=0,t2=0;
for(int num:nums)
{
if((lsb&num)!=0)
{
t1^=num;
}else
{
t2^=num;
}
}
if(t1>t2)
{
return new int[]{t2,t1};
}
return new int[]{t1,t2};
}其他算法部分
构建乘积数组
此题思路也无敌,但我没看懂,二刷的时候再看看吧
public int[] multiply (int[] A) {
// write code here
int[]B=new int[A.length];
B[0]=1;
for(int i=1;i<A.length;i++)
B[i]=B[i-1]*A[i-1];
int temp=1;
for(int i=A.length-1;i>=0;i--)
{
B[i]*=temp;
temp*=A[i];
}
return B;
}第一个只出现一次的字符
考察方法的
public int FirstNotRepeatingChar (String str) {
// write code here
for(int i=0;i<str.length();i++)
{
if(str.lastIndexOf(str.charAt(i))==i&&str.indexOf(str.charAt(i))==i)
{
return i;
}
}
return -1;
}调整数组顺序使奇数位于偶数前面(一)
这题目南软有一种快速排序的方法,但我我忘了
方法一:就是建新数组
public int[] reOrderArray (int[] array) {
// write code here
int n=array.length;
int []res=new int[n];
int odd=0;
for(int i=0;i<n;i++)
{
if(array[i]%2==1)
odd++;
}
int x=0,y=odd;
for(int i=0;i<n;i++)
{
if(array[i]%2==1)
{
res[x]=array[i];
x++;
}
else
{
res[y]=array[i];
y++;
}
}
return res;
}方法二:原地排序,先鸽了
//鸽了把数组排成最小的数
思路:对于string类型,a+b>b+a的话,那么就排序
public String PrintMinNumber (int[] numbers) {
// write code here
if(numbers==null||numbers.length==0)
return "";
String[]nums=new String[numbers.length];
for(int i=0;i<numbers.length;i++)
nums[i]=numbers[i]+"";
Arrays.sort(nums,new Comparator<String>(){//重写compare函数
public int compare(String s1,String s2){
return (s1+s2).compareTo((s2+s1));//规则是:返回值大于0则交换
//String.compareto:如果左大于右,则返回大于0的值
//跟这里需求是一样的,把大的换到后面
}
});
StringBuilder res=new StringBuilder();
for(int i=0;i<nums.length;i++)
res.append(nums[i]);
return res.toString();
}整数中1出现的次数(从1到n整数中1出现的次数)
我的评价:看k神的题解,背下来
public int countDigitOne(int n) {
int digit=1,res=0;
int high=n/10,cur=n%10,low=0;
while(high!=0||cur!=0)
{
if(cur==0)res+=high*digit;
else if(cur==1)res+=high*digit+low+1;
else res+=(high+1)*digit;
low+=cur*digit;
cur=high%10;
high/=10;
digit*=10;
}
return res;
}和为S的连续正数序列
滑动窗口法,简直是天才
public ArrayList<ArrayList<Integer>> FindContinuousSequence (int sum) {
// write code here
//滑动窗口法,大了就左边出去,小了就右边进来
ArrayList<ArrayList<Integer>> res=new ArrayList<>();
int low=1,high=2;
while(low<high)
{
int cur=(high+low)*(high-low+1)/2;//计算和
if(cur==sum)
{
ArrayList<Integer> list=new ArrayList<>();
for(int i=low;i<=high;i++)
{
list.add(i);
}
res.add(list);
low++;
}
else if(cur<sum)
{
high++;
}
else
{
low++;
}
}
return res;
}和为S的两个数字
我的误区:还是l=0,r=1去滑动窗口,但是这样不对
应该r=最末尾的地方,这样可以避免什么,避免你们从同一侧向右,然后r++,而l又要从0开始遍历,那不就相当于两层for了吗
public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
ArrayList<Integer> res = new ArrayList<Integer>();
//左右双指针
int left = 0, right = array.length - 1;
//对撞双指针
while(left < right){
//相加等于sum,找到目标
if(array[left] + array[right] == sum){
res.add(array[left]);
res.add(array[right]);
break;
//和太大,缩小右边
}else if(array[left] + array[right] > sum)
right--;
//和太小,扩大左边
else
left++;
}
return res;
}打印从1到最大的n位数
public int[] printNumbers (int n) {
// write code here
int size=1;
while(n>0)
{
size=size*10;
n--;
}
int[]res=new int[size-1];
for(int i=1;i<size;i++)
{
res[i-1]=i;
}
return res;
}暴力,没啥可说的
丑数
思路:所以我们就将res[i]去乘以 2、3、5,然后比较出最小的那个,就是我们当前的下一个丑数了。
但是前面有那么多数,如何比较呢,维护i2,i3,i5
public int GetUglyNumber_Solution (int index) {
// write code here
if(index<=6)return index;
int i2=0,i3=0,i5=0;//从1开始,每个丑数都需要乘一次2,3,5
//i2,i3,i5代表的就是从1开始,每个丑数乘2,3,5
int[] res=new int[index];
res[0]=1;//1是第一个丑数
for(int i=1;i<index;i++)
{
res[i]=Math.min(res[i2]*2,Math.min(res[i3]*3,res[i5]*5));
if(res[i]==res[i2]*2)//如果这一次被选择的是i2上的数乘2,那么i2++
i2++;
if(res[i]==res[i3]*3)
i3++;
if(res[i]==res[i5]*5)
i5++;
}
return res[index-1];
}孩子们的游戏(圆圈中最后剩下的数)
想起来一个思路了,那就是倒过来推,推出剩下的那个在原来全员都在的情况下,他的下标是什么
这题还不能用模拟,因为会超时
我们看力扣题解里的”换个角度理解xxx”
制定规则:当去除一个人之后,把去除的那个人的后一个人作为下标0,然后去除的人的前面的人 全部排到后面去
只剩最后一个人的时候,他的下标必定是0,然后我们反推出他在人全在的时候下标是哪个
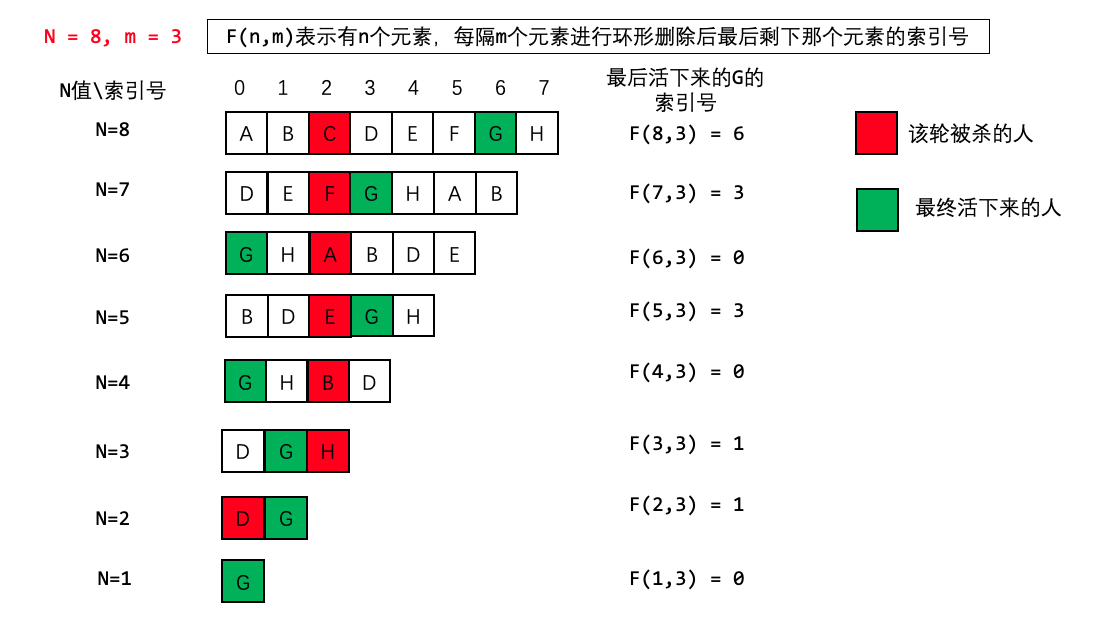
正过来:先删除,然后左移m-1位
反过来:先加回去,然后右移m位,如果溢出了,就加到最前面
反过来的公式:[当前位置+m(右移m位)]%i(如果溢出就加到最前面) i是当前有多少个数字
public int iceBreakingGame(int num, int target) {
int pos=0;//最后剩下下标肯定是0
for(int i=2;i<=num;i++)
{
pos=(pos+target)%i;
}
return pos;
}字符流中第一个不重复的字符_牛客题霸_牛客网 (nowcoder.com)
第一种弱智方法:
public class Solution {
//Insert one char from stringstream
HashMap<Character,Integer>map=new HashMap<>();
StringBuilder s=new StringBuilder();
public void Insert(char ch)
{
map.put(ch,map.getOrDefault(ch,0)+1);
s.append(ch);
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce()
{
for(int i=0;i<s.length();i++)
{
if(map.get(s.charAt(i))==1)
{
return s.charAt(i);
}
}
return '#';
}
}第二种:用linkedHashmap的有序性
public class Solution {
//Insert one char from stringstream
private Map<Character,Integer>map=new LinkedHashMap<>();
public void Insert(char ch)
{
if(map.containsKey(ch))
{
map.put(ch,map.get(ch)+1);
}else
{
map.put(ch,1);
}
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce()
{
for(Map.Entry<Character,Integer>set:map.entrySet())
{
if(set.getValue()==1)
{
return set.getKey();
}
}
return '#';
}
}比第一种快了一半
LCR 138. 有效数字 - 力扣(LeetCode)
y用宫水三叶的方法模拟
class Solution {
//按照宫水三叶的思路,先进行处理,然后分情况判断,如果有E,那就分别判断左右,没有就整体判断
//然后我们把所有的e换成E
//小数:就是小数点的左右至少有一方有数字
//整数:至少有一位数字
//E的左边可以是整数和小数,右边必须是整数
public boolean validNumber(String s) {
s=s.trim();
int n=s.length(),l=0,r=n-1;
s=s.replace('e', 'E');
int idx=0;
while(idx<n&&s.charAt(idx)!='E')idx++;
if(idx==n)
{
return check(s, true);
}else
{
return check(s.substring(0,idx), true)&&check(s.substring(idx+1), false);
}
}
public boolean check(String s ,boolean isDecimal)
{
if(s.equals(".")||s.equals(""))return false;//这一半只有个符号和空,那就false
int n=s.length();
boolean once=true;//是不是只有一个小数点
for(int i=0;i<n;i++)
{
char c=s.charAt(i);
if(c=='+'||c=='-')
{
if(i!=0||i==n-1)return false;
}else if(c=='.')
{
if(!isDecimal)//不被允许有小数的部分
{
return false;
}
if(!once)return false;//已经出现过小数点了
once=false;
boolean a=i-1>=0&&Character.isDigit(s.charAt(i-1));//左边是不是数字
boolean b=i+1<n&&Character.isDigit(s.charAt(i+1));//右边是不是数字
if(!(a||b))return false;
}else if(!Character.isDigit(c)){
return false;
}
}
return true;
}
}LCR 131. 砍竹子 I - 力扣(LeetCode)
数学结论:尽量以长度3切,这样最大
public int cuttingBamboo(int n) {
if(n<4)return n-1;
int res=1;
while (n>4) {
res*=3;
n-=3;
}
return res*n;
}LCR 132. 砍竹子 II - 力扣(LeetCode)
还是和上一题一样的思路,只不过在循环过程和最后要取模
public int cuttingBamboo(int n) {
if(n<4)return n-1;
long res=1;
while(n>4)
{
res=res*3%1000000007;
n-=3;
}
return (int)(res*n%1000000007);
}\
//积的结果取余等于 每个乘数取余的乘积再取余但是在牛客里,这样的方法会超时,我们采用快速幂的方法,可以将时间复杂度降低
回溯
79. 单词搜索 - 力扣(LeetCode)
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length, w = board[0].length;
boolean[][] visited = new boolean[h][w];
for(int i=0;i<h;i++)
{
for(int j=0;j<w;j++)
{
boolean flag=check(board,visited,i,j,word,0);
if(flag)
{
return true;
}
}
}
return false;
}
public boolean check(char[][]board,boolean[][]visited,int i ,int j,String s,int k)
{
if(board[i][j]!=s.charAt(k))
{
return false;
}else if(k==s.length()-1)//长度一样了
{
return true;
}
visited[i][j]=true;
boolean result=false;
int[][]dirs={{0,1},{0,-1},{1,0},{-1,0}};
for(int[]dir:dirs)
{
int newi=i+dir[0],newj=j+dir[1];
if(newi>=0&&newi<board.length&&newj>=0&&newj<board[0].length)
{
if(!visited[newi][newj])
{
boolean flag=check(board,visited,newi,newj,s,k+1);//递归查询他周边的
if(flag)
{
result=true;//说明这条路径可以找到
break;//不用再找了
}
}
}
}
visited[i][j]=false;//回溯
return result;
}
}应该要知道flag是什么用处?是用来剪枝的,就是说找到了 一条路径后,直接设置flag为true,退出整个搜索过程
LCR 130. 衣橱整理 - 力扣(LeetCode)
这个比上一题简单啊,我草
class Solution {
public int wardrobeFinishing(int m, int n, int cnt) {
int res=0;
boolean[][]visited=new boolean[m][n];
return dfs(visited, m, n, cnt, 0, 0);
}
public int dfs(boolean[][]visited,int m,int n,int cnt,int i,int j)
{
if(i>=m||j>=n||sums(i)+sums(j)>cnt||visited[i][j])return 0;
visited[i][j]=true;
return 1+dfs(visited,m,n,cnt,i+1,j)+dfs(visited, m, n, cnt, i, j+1);
}
int sums(int x)
{
int s=0;
while (x!=0) {
s+=x%10;
x=x/10;
}
return s;
}
}为什么这题不用回溯?就是不用啊

